Coding Challenge: Implementing QuickSort in Ruby

Lately I've been trying to challenge myself by taking a stab at some common coding questions asked in software engineering job interviews. After years of working on apps you would think that this kind of thing comes easy, but software development in the modern age comes with a heavy side of Googling and lookup, so challenging your brain in this way to implement an algorithm or process from just its definition is good practice to keep you sharp.

Previously, I had implemented MergeSort in Ruby, so today I am going to take the next step and implement the faster QuickSort algorithm.

I'll present all code in this post as easy-to-read Ruby code, and I will also try to avoid some of the obscure language shortcuts to make the method more clear.

In order to implement an algorithm in any language, you need to understand it, so here is where I needed to lookup a high level description of how QuickSort works again:

Quick sort is a highly efficient sorting algorithm and is based on partitioning of array of data into smaller arrays. A large array is partitioned into two arrays one of which holds values smaller than the specified value, say pivot, based on which the partition is made and another array holds values greater than the pivot value. Quick sort partitions an array and then calls itself recursively twice to sort the two resulting subarrays. Tutorials Point

Sounds a little more complicated, but similar to the MergeSort algorithm. First, let's define a recursive method to call and setup a simple test to see if it is working:

def quick_sort(array)
  array
end

unsorted_array = (1..10).to_a.shuffle
time1 = Time.now
sorted1 = quick_sort(unsorted_array.dup)
time2 = Time.now
puts "QUICK_SORT SORTED CORRECTLY: #{sorted1 == unsorted_array.sort}\n#{time2 - time1}sec\nunsorted: #{unsorted_array}\n sorted: #{sorted1}\n\n"

Obviously, this will fail, returning the original array immediately. Running it produces our failure output:

QUICK_SORT SORTED CORRECTLY: false
4.0e-06sec
unsorted: [1, 4, 9, 8, 3, 6, 10, 5, 2, 7]
sorted: [1, 4, 9, 8, 3, 6, 10, 5, 2, 7]

However, now that we have a basic test for success, we can begin implementing the algorithm. As a divide-and-conquer algorithm, we need to figure out how to divide the array passed in. MergeSort is also a divide-and-conquer algorithm, and the divide function is very basic: simply split the array in half. QuickSort uses a pivot, and that pivot is used to partition the array into two new arrays that have values less-than-or-equal-to the pivot, and greater-than the pivot. Normally, this partitioning is done in-place in the array by keeping track of indices and swapping spots. But, I'm going to start with a more inefficient way of implementing QuickSort, just to get the naive version up and running.

There are various ways to choose the pivot. Some choose randomly, some choose the first element of the array, I find it easier conceptually to choose the last item in the array. So first, we will get the value of the pivot for comparison in out partitioning.

def quick_sort(array)
  pivot = array.pop
end

Once we have the pivot, we need to go through the entire array, putting elements in either a left array representing values <= pivot, or a right array representing values > pivot.

def quick_sort(array)
  pivot = array.pop
  left, right = [], []
  for value in array
    value <= pivot ? left.push(value) : right.push(value)
  end
end

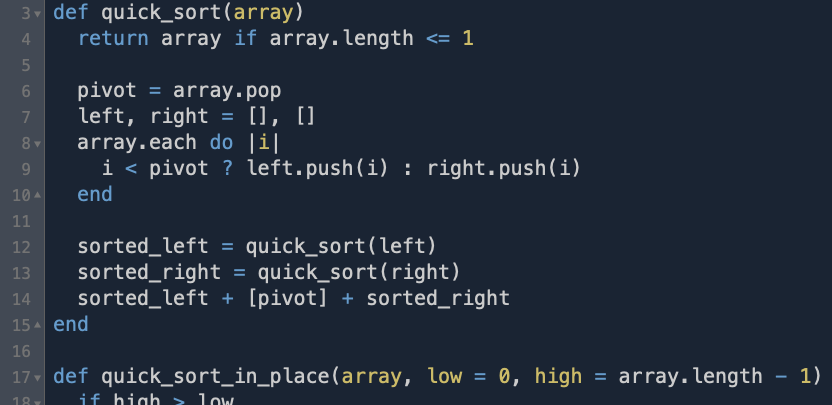
Now that we have two subarrays representing values <= pivot and > pivot>, we recurse by calling quick_sort again on the subarray, and combining them with the pivot once done.

def quick_sort(array)
  pivot = array.pop
  left, right = [], []
  for value in array
    value <= pivot ? left.push(value) : right.push(value)
  end
  quick_sort(left) + [pivot] + quick_sort(right)
end

Of course, with recursion, this method would go on forever without a base case, so let's add that. Because each array passed into the recursive call is smaller than the original, we would eventually get to a spot where we see an array of either 1 or 0 elements, each of which would already be in the correct sorted order. So the base case is to simply return that array without recursing. Adding it, we get:

def quick_sort(array)
  if array.length > 1
    pivot = array.pop
    left, right = [], []
    for value in array
      value <= pivot ? left.push(value) : right.push(value)
    end
    array = quick_sort(left) + [pivot] + quick_sort(right)
  end
  array
end

Testing it out, we see that it passes.

QUICK_SORT SORTED CORRECTLY: true
1.5e-05sec
unsorted: [5, 8, 3, 9, 6, 2, 4, 1, 7, 10]
sorted: [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

How about running it on a much larger array, say 1000000 (1M) numbers? I'll run it without printing the arrays, to save my machine's output buffer.

unsorted_array = (1..1000000).to_a.shuffle
time1 = Time.now
sorted1 = quick_sort(unsorted_array.dup)
time2 = Time.now
puts "QUICK_SORT SORTED CORRECTLY: #{sorted1 == unsorted_array.sort}\n#{time2 - time1}sec\n\n"

QUICK_SORT SORTED CORRECTLY: true
3.08712sec

That's already blazing fast, but now I'm curious if I can get speed benefits from doing the in-place method that other people have implemented. This is a little trickier to implement due to having to keep track of indices as you move through the partitioning process, but it has the benefits of saving memory by always working in-place and not having to allocate new arrays all over the call stack. Let's dive in.

Starting with a new quick_sort_in_place method that will accept and array, and the indices to sort:

def quick_sort_in_place(array, low = 0, high = array.length - 1)
  array
end

For the rest, we will still choose the pivot as the last item, but we need to now partition the array around it in-place before recursing. Because we are not allocating new arrays, we will also need to pass in the desired "subarray" to the recursive call, meaning we are defining the subarray by start and end indices on the original array. To make the method cleaner, we will pull out the partitioning logic into a helper method which takes an unsorted array with low and high indices, and moves items around the array so that the partition is in the correct, permanent spot, the elements to its left are lower or equal, and the elements to the right are higher.

def partition(array, low, high)
  pivot = array[high]
  dividing_index = low

  (low...high).each do |index|
    value = array[index]
    if value <= pivot
      # Swap the value into the "low" partition, and increment the dividing_index
      array[index] = array[dividing_index]
      array[dividing_index] = value
      dividing_index +=1
    end
  end
  # Swap the lowest "high" value with the pivot
  array[high] = array[dividing_index]
  array[dividing_index] = pivot
  dividing_index
end

This starts by moving our way across the entire array range from low to high not including high (notice the ruby non-inclusive range operator ...). We don't use the high value because it is our pivot! At each index of the array, we check whether the value at that position is <= pivot, and if it is, we need to put it at the end of the "low" section, indicated by the variable dividing_index. We keep this pointer to the end of the "low" section (initialized with no length at low) so that we can know where to place a lower value, if we see one. Because this is an in-place algorithm, we need to swap the position of the lower value and the higher value already at the dividing_index. This happens all the way up to the pivot (at the high index), at which point we need to swap out whatever value is the first "high" partition with the pivot. Finally, we return the index of the pivot, already placed into its final position in the sorted array.

Armed with a partitioned array where each value below the pivot index is less-than-or-equal-to the pivot, and every value to the right of the pivot index is greater-than the pivot, we can recurse on those smaller arrays.

def quick_sort_in_place(array, low = 0, high = array.length - 1)
  pivot = partition(array, low, high)
  quick_sort_in_place(array, low, pivot - 1)
  quick_sort_in_place(array, pivot + 1, high)
  array
end

Just like before however, we need a base case. Here, this is defined by the size of the array to handle smaller values passed in initially, but more importantly, by the low and high indices passed in. If the subarray we are looking at is larger than 1, then we should recurse. Otherwise we are done.

def quick_sort_in_place(array, low = 0, high = array.length - 1)
  if high > low
    pivot = partition(array, low, high)
    quick_sort_in_place(array, low, pivot - 1)
    quick_sort_in_place(array, pivot + 1, high)
  end
  array
end

Now that it is all written, we need a test to compare the ss:

unsorted_array = (1..1000000).to_a.shuffle
time1 = Time.now
sorted1 = quick_sort(unsorted_array.dup)
time2 = Time.now
sorted2 = quick_sort_in_place(unsorted_array.dup)
time3 = Time.now
puts "QUICK_SORT SORTED CORRECTLY: #{ sorted1 == unsorted_array.sort}\n#{time2 - time1}sec\n\n"#"\n\n#{unsorted_array}\n\n#{sorted1}\n\n"
puts "QUICK_SORT_IN_PLACE SORTED CORRECTLY: #{sorted2 == unsorted_array.sort}\n#{time3 - time2}sec\n\n"#"\n\n#{unsorted_array}\n\n#{sorted2}"

And running this test with one million items, we see that the in-place QuickSort algorithm is not only faster, but also (by-definition) uses fewer memory resources as well.

QUICK_SORT SORTED CORRECTLY: true
3.416708sec

QUICK_SORT_IN_PLACE SORTED CORRECTLY: true
2.633779sec

That being said, I would probably still choose the first QuickSort algorithm, for its readability over the second unless this method was part of an absolutely time-critical pathway. Dealing directly with array indices always has me feeling like and off-by-one error could creep in, and they are just harder to debug (at least with my ruby-oriented brain). Which one would you use? Are there other solutions which are both fast, in-place, and still readable?

Was this page helpful for you? Buy me a slice of 🍕 to say thanks!