Coding Challenge: Implement a Square Root Function

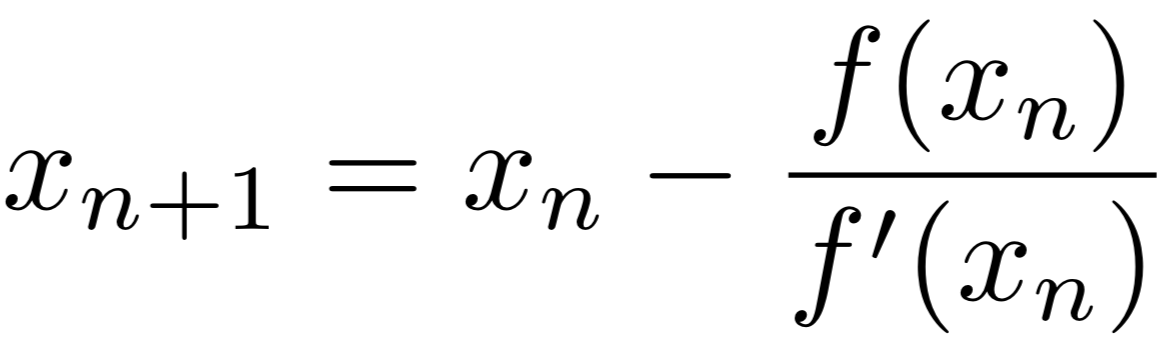
(not the sqrt function)

Lately I've been trying to challenge myself by taking a stab at some common coding questions asked in software engineering job interviews. After years of working on apps you would think that this kind of thing comes easy, but software development in the modern age comes with a heavy side of Googling and lookup, so challenging your brain in this way to implement an algorithm or process from just its definition is good practice to keep you sharp.

Yesterday, I came across a question which was rated on LeetCode as EASY and decided to give it a go, finding that the optimal answer was anything but easy. The question was:

Implement int sqrt(int x).
  - Compute and return the square root of x, where x is guaranteed to be a non-negative integer.
  - Since the return type is an integer, the decimal digits are truncated and only the integer part of the result is returned.

Here's how I naively implemented that in ruby.

After racking my brain for a bit and trying to see if I could do some sort of division/multiplication/operation to alternatively deduce the square root of a number, I was stumped. The only way I could think of was a naive brute-force way, where I would multiply numbers together iteratively starting with i=1 until the result was larger than the input value x. Let's start there.

# @param {String} input
# @return {Integer}
def my_sqrt_naive(x)
  return x if x == 0

  i = 0
  i += 1 while i*i <= x
  return i-1
end

And a test suite:

failed = []
num_tests = 2**20
t1 = Time.now
for i in (0..num_tests)
  failed << i if Math.sqrt(i).floor != my_sqrt_naive(i)
end
t2=Time.now
if failed.empty?
  puts "SUCCESS over #{num_tests} tests in #{t2-t1}s"
else
  puts "FAILURE over #{num_tests} tests in #{t2-t1}s: #{failed}"
end

SUCCESS over 1048576 tests in 14.746733s

While on LeetCode, when I submitted this solution, it was accepted and all tests passed, however it mentioned that 90% of other ruby submissions were faster than mine. I couldn't think of any other way to approach this at the time, but I was bothered by the fact that the brute-force answer is usually not the best answer, and others had clearly found a faster, better answer. I had to do some sleuthing on the net to find a better way, one that may have been obvious to new grads who had taken math courses much more recently than I have.

It turns out that good ol' Sir Isaac Newton had a method for approximating any function by using its derivative. I won't get into the technical math components of why this works, but if you want to know, here is a MIT paper on it. There are also plenty of videos on YouTube explaining how and why it works that you can check out. The astute reader may have noticed this image already at the top of the article, but Newton's formula boils down to this:

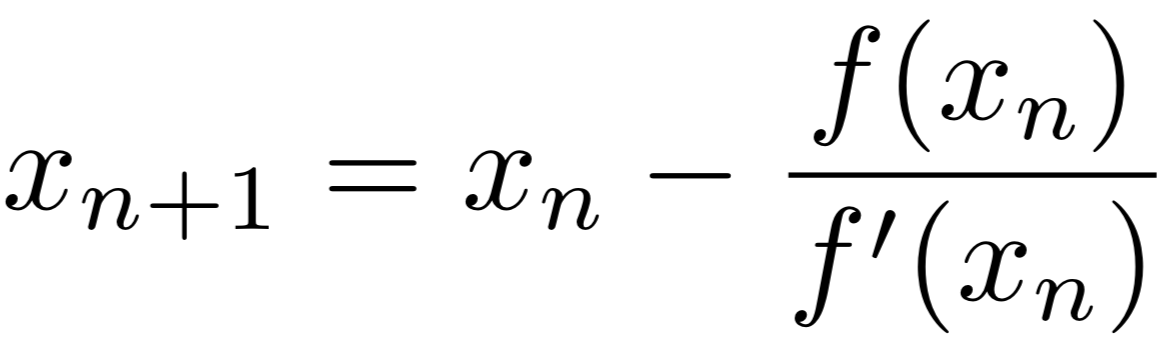
The formula basically says that a better, closer, next guess xn+1 is equal to your previous best guess xn minus the ratio of the function your are trying to solve for using your guess f(xn), and the derivative of that function using your guess f'(xn)

The formula is generalized for any function, but we want to apply it specifically to the function that will help us here, meaning the inverse of the sqrt function. Since we are told to return a value, say y that is the floor of the sqrt(x), we are left with the following equation:

y = sqrt(x)
f(y) = y - sqrt(x)
f(y) = y^2 - x

f'(y) = 2y

In those equations, we are given x as an input, and y is our guess. Let's put it into a method to see how it will work.

# @param {String} input
# @return {Integer}
def my_sqrt_newton(x)
  return x if x == 0

  guess = x
  new_guess = (guess - (guess**2 - x) / (2.0 * guess))

  return new_guess.floor
end

This result uses a horrible initial first guess as the number we are trying to find the square root of, but it is a starting point, and Newton's method converges pretty quickly to the right answer so we will leave it. Besides, it's the right answer for 1 anyway. We don't want to leave the method after getting only 1 guess correction, so we need a while loop, but what will we check against to know when to stop?

Since we are told we can return the floor integer value of any fractional result, this means that we can iterate until the absolute value of the difference between the previous guess and the new guess is less than 1. Putting in that while loop and stop condition:

def my_sqrt_newton(x)
  return x if x == 0

  guess = x
  diff = 2**31 - 1

  while diff >= 1
    new_guess = (guess - (guess**2 - x) / (2.0 * guess))
    diff = (new_guess - guess).abs
    guess = new_guess
  end

  guess.floor
end

Running this against our test suite, I would expect it to not only succeed, but be much, much faster…

SUCCESS over 1048576 tests in 2.445359s

…and it was, by an order of magnitude! Genius Sir Issac Newton comes to the rescue! Do you see a faster way?

Was this page helpful for you? Buy me a slice of 🍕 to say thanks!